|
Come si legge spesso nei capitoli introduttivi riguardo le basi della fotografia, l’esposizione in fotografia può essere associata alla quantità di acqua erogata da un rubinetto, in funzione di quanto questo viene aperto (apertura diaframma), per quanto tempo (tempo di scatto) e della pressione (ISO). L'esposizione può essere mantenuta fissa se si variano reciprocamente tempo di scatto e aperta di diaframma, mantenendo gli ISO costanti. Ad esempio, scattare ad 1/100 di secondo con apertura f/2.8 equivale a scattare ad 1/50 di secondo con apertura f/4. Questo, però, è valido solo per quanto riguarda l’esposizione alla luce, ovvero la quantità di fotoni che raggiungono il sensore (o la pellicola). Le immagini complessive saranno, invece, diverse per quanto riguarda la così detta profondità di campo (pdc), ovvero le porzioni della scena che saranno nitide e sfocate. La figura 1 mette in evidenza il tipico esempio della variazione delle zona nitida e delle zone sfuocate in funzione dell'apertura diaframma. Vedremo di seguito che esistono anche altre variabili che hanno influenza sulla pdc e cercheremo soprattutto si mettere in luce i principi che le governano.
Figura 1 Esempio della variazione della pdc in funzione dell'apertura diaframma
Circolo di confusione e profondità di fuoco
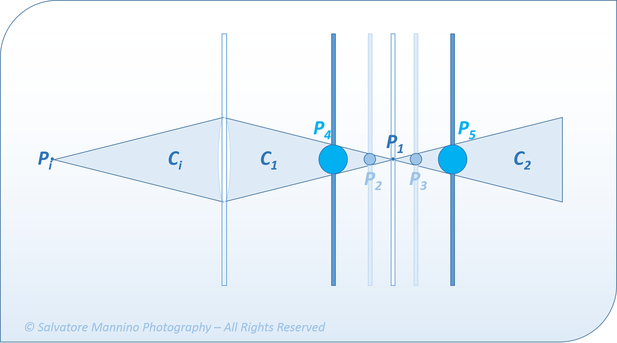
Per capire in fondola profondità di campo, è bene conoscere alcuni concetti che ne sono alla base. La profondità di fuoco è un concetto di questi che non può prescindere dalla teoria del circolo di confusione. Per comprendere questa teoria, si consideri lo schema mostrato in figura 2. Si parta da ciascun punto P di un qualsiasi degli infiniti piani di una scena. La luce viene riflessa da tale punto P in tutte le direzioni, ma solo quelle che definiscono un cono solido Ci, con base corrispondente all’apertura del diaframma, saranno catturate dalla fotocamera. Le varie lenti interne dell’obbiettivo raddrizzano questo cono creandone un secondo C1, con vertice nel punto P1 corrispondente al punto P. Dal punto P1 parte, a sua volta, un ulteriore cono C2. Se si pone il piano del sensore (o pellicola) in corrispondenza del punto P1, P sarà a fuoco. Tutti i punti lontani da Pi verranno riprodotti come cerchi. Alcuni di questi sembreranno, all'occhio umano, ancora a fuoco mentre altri no. Ciò dipende dal potere risolutivo dell’occhio: tutti i circoli di dimensioni minori del potere risolutivo dell’occhio umano saranno percepiti come punti e sembreranno quindi a fuoco, mentre tutti i circoli di dimensione maggiore saranno percepiti come tali e quindi come sfocatura dei rispettivi punti nativi. È questa la teoria del circolo di confusione. Il potere risolutivo dell’occhio umano è circa 0,1 mm.
Figura 2 Schema della proiezione di una lente di un punto Pi generico
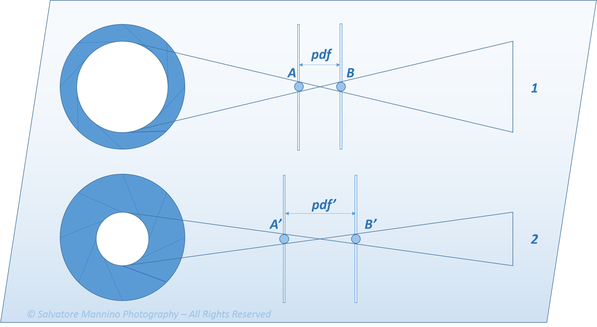
Può sembrare empirico il fatto che chiudendo l’apertura del diaframma aumenti la “quantità” di scena nitida. Tutto ciò dipende proprio dalla teoria del circolo di confusione, ed è mostrato in modo esemplificativo in figura 3. Considerando il caso 1, posizionando il sensore all’interno dell’intervallo A-B, l’immagine resterà nitida in quanto al di sotto del limite risolutivo umano. Posizionando, invece, il sensore appena fuori da tale intervallo, l’immagine risulterà sfuocata all’occhio perché i cerchi non saranno percepiti più come puntini, bensì come cerchi. I limiti A e B definiscono, quindi, la profondità di fuoco. Quando si riduce l’apertura del diaframma, si riduce l’angolo solido per ogni punto catturato dalla fotocamera. In tal modo aumenta, quindi, il numero di piani con circoli di dimensioni inferiori ai due limiti A’ e B’ e si avrà una profondità di fuoco maggiorata. In condizioni di pdf maggiori, errori nella messa a fuoco avranno ripercussioni minori sulla nitidezza finale dell’immagine. Viceversa, a grandi aperture di diaframma e quindi valori di pdf minori, l’accuratezza nella messa a fuoco è fondamentale.
Figura 3 Rappresentazione schematica della variazione della profondità di fuoco
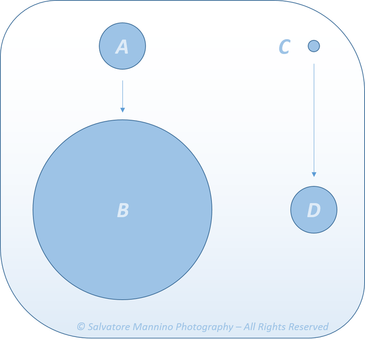
Continuiamo ad analizzare il concetto di circolo di confusione. Si consideri la figura 4. Per un circolo di confusione al limite di risoluzione dell’occhio umano ovvero di 0,1 mm (A), se venisse ingrandito di 4 volte (B) supererebbe tale limite e non verrebbe percepito più come punto bensì come circolo, appunto. L’immagine sembrerebbe, allora, sfuocata. Considerando, quindi, l’ingrandimento di 4 volte, il circolo dovrebbe avere dimensione massima di 0,025 mm per rimanere all’interno del limite ed essere percepito come punto anche a seguito dell’ingrandimento.
Figura 4 Rappresentazione dell'ingrandimento del circolo di confusione
Detto ciò, si pensi adesso a quando si sviluppa e si stampa una fotografia da pellicola. Si utilizza l’ingranditore che porta l’immagine dalla dimensione della diapositiva a quella della carta fotografica utilizzata. Stesso discorso vale per il digitale quando si ingrandisce la foto dalla dimensione del sensore. Ingrandendo l’immagine, si ingrandisce allo stesso tempo il circolo di confusione. Se si immagina di fare un ingrandimento di circa 10 volte, i circoli di confusione al valore limite di 0,1 mm diventeranno di circa 1 mm. Secondo quanto appena visto, viene da pensare che, per apprezzare l’immagina ancora in modo nitido, si dovrebbe diminuire il valore limite iniziale del circolo di confusione da 0,1 a 0,01 mm per non risentire dell’ingrandimento. Si dovrebbe, quindi, calcolare di volta in volta il valore del circolo di confusione in funzione dell’ingrandimento finale? In realtà questo non è necessario, poiché ciò che conta è il valore finale impresso sulla retina dell’occhio umano. Infatti, un’immagine ingrandita, che vista da vicino sembra fuori fuoco, diventa sempre più nitida quando più ci si allontana e la si guarda da distanze maggiori. Come mostrato in figura 5, la distanza di visione riduce l’angolo di percezione di ogni singolo punto riducendo così il circolo di confusione impresso sulla retina, compensando il suo aumento nella stampa ingrandita.
Figura 5 Influenza della distanza di osservazione sul circolo di confusione percepito
La profondità di campo
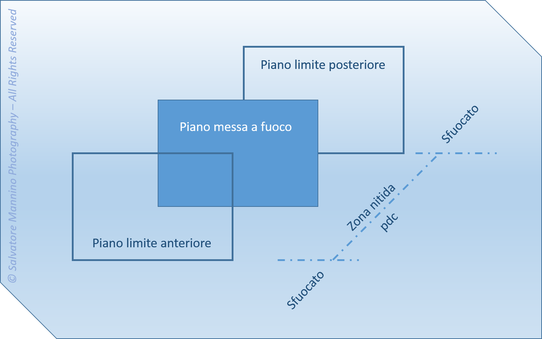
Quanto visto finora pone le basi per capire da cosa nasce la profondità di campo. La profondità di campo (pdc), empiricamente, consiste nel fatto che, quando si mette a fuoco un determinato piano verticale di una scena, risulteranno a fuoco anche una certa quantità prima e un’altra quantità dopo il piano di messa a fuoco, come schematizzato in figura 6.
Figura 6 Rappresentazione schematica della profondità di campo
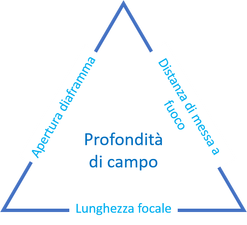
La pdc può diminuire o aumentare da qualche millimetro fino ad infinito in funzione di 3 fattori (figura 7): apertura diaframma, distanza di messa a fuoco, lunghezza focale dell’obbiettivo.
Figura 7 Triangolo della profondità di campo
Apertura diaframma
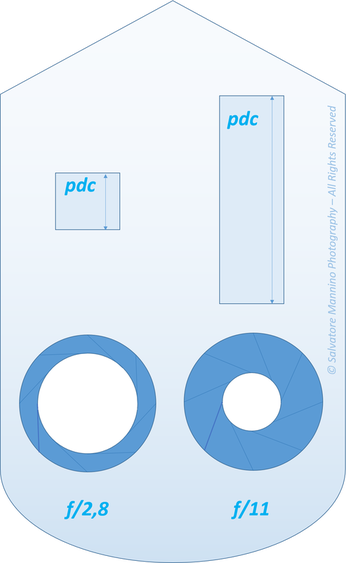
Pdc e apertura diaframma sono inversamente proporzionali: più si chiude il diaframma maggiore sarà la porzione di spazio nitida (figura 8).
Figura 8 Influenza dell'apertura diaframma sulla pdc
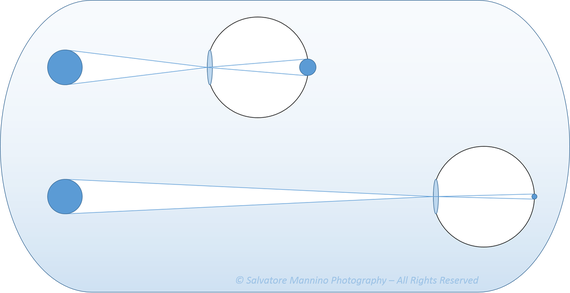
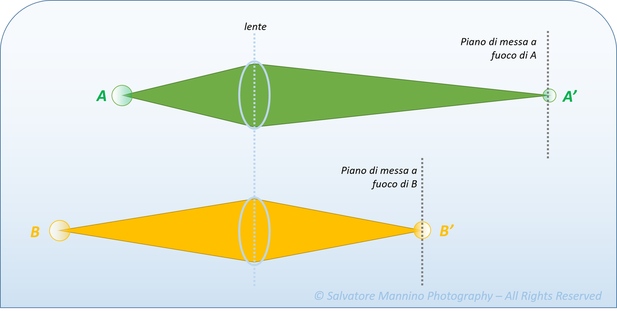
Si presti adesso particolarmente attenzione per comprendere la ragione fisica che sta dietro a tale concetto, per far sì che non rimanga di natura empirica. Si prenda per assodato (per il momento) che oggetti vicini hanno piani di messa a fuoco più indietro rispetto ad oggetti lontani. Questo vuol dire che, più un oggetto si allontana, più la sua immagine nitida si forma vicino la lente. Come mostrato in figura 9, il punto A è più vicino alla lente rispetto al punto B, e la sua immagine nitida A’ viene formata più indietro rispetto a B’.
Figura 9 Schema di proiezione di punti lontani e punti vicini
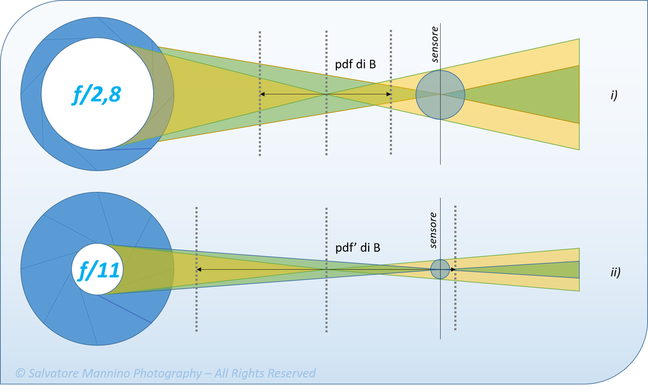
Consideriamo il caso i) della figura 10. Se mettiamo a fuoco il punto A con apertura diaframma f2,8, il piano del sensore si troverà perfettamente sul vertice del cono verde. In queste condizioni, il sensore taglia il cono giallo del punto B lontano dal vertice, e il circolo riflesso B’ avrà dimensioni maggiori al limite del circolo di confusione risultando così sfuocato. In queste condizioni la pdf per il punto B è piccola e la pdc risulta essere insufficiente per renderlo nitido.
Se chiudiamo il diaframma a f11 come nel caso ii), aumenta la pdf di B. Adesso il sensore, ancora a fuoco su A, interseca il cono giallo su valori per i quali il circolo riflesso B’ ha dimensioni inferiori al limite del circolo di confusione. In queste condizioni anche il punto B sarà percepito in maniera nitida come il punto A. La pdc è stata aumentata.
Figura 10 Rappresentazione schematica dell'influenza dell'apertura diaframma sulla pdc
La pdc può essere calcolata tramite formule matematiche. In passato sono state create delle tavole da poter consultare; anche la maggior parte dei vecchi obbiettivi porta su di essi delle scale per poter scegliere la pdc in fase di scatto. Oggi è possibile consultare diverse applicazioni digitali sui propri smartphone/tablet. Basta impostare i valori relativi al triangolo della pdc: apertura diaframma, lunghezza focale e distanza di messa a fuoco. In realtà va impostato un quarto parametro: la dimensione sensore, vedremo dopo il perché.
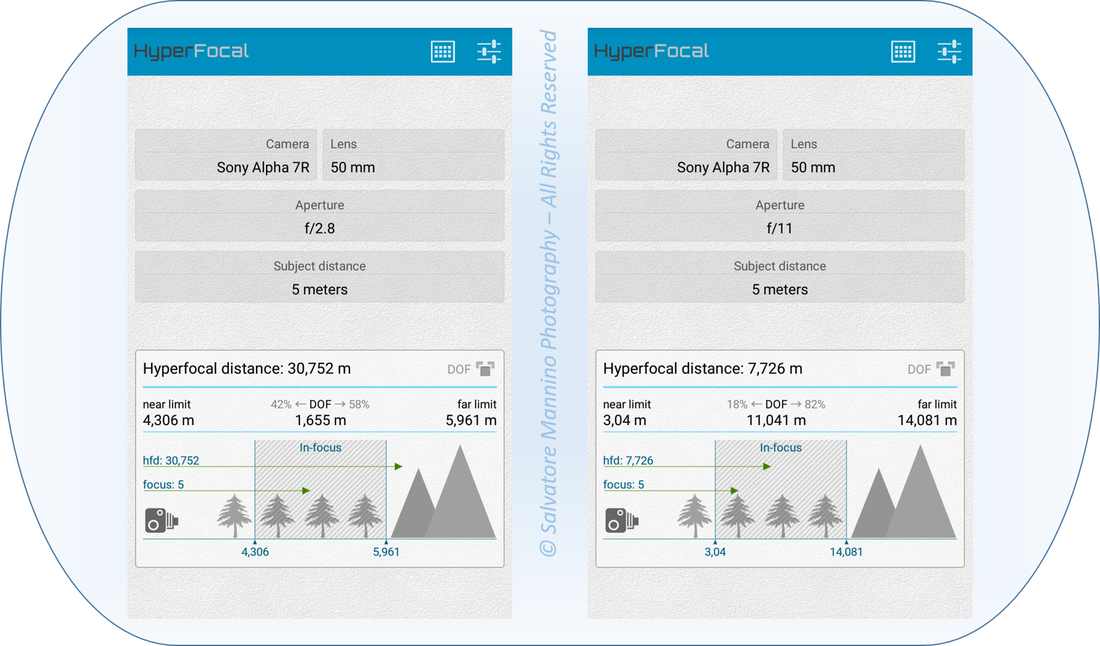
In figura 11 viene mostrato un esempio ottenuto con l’applicazione HyperFocal Pro. Hyperfocal Pro è una app molto completa disponibile gratuitamente sul market Android e verrà approfondita successivamente in tutte le sue potenzialità. Impostiamo prima di tutto il tipo di fotocamera (per la dimensione sensore), nel nostro caso si è scelto la Sony a7r ovvero il formato 35 mm. Manteniamo fissi i valori di lunghezza focale e distanza di messa a fuoco rispettivamente a 50 mm e 5 m. Considerando un’apertura diaframma f 2,8 si ottiene una pdc di 1,655 m, con limite anteriore a 4,306 m e limite posteriore a 5,961 m. Chiudiamo il diaframma a f 11. La pdc aumenta a 11,041 m ovvero di quasi il 570% o se preferite, a f 2,8 era circa l’85% in meno! Oltre a cambiare il valore assoluto di pdc, che passa da circa 1,6 a 11 metri, è anche la sua distribuzione attorno il piano di messa a fuoco a cambiare! Infatti, a f 2,8 si vede come la zona nitida si estende per:
Figura 11 Confronto della scelta dell'apertura diaframma tramite HyperFocal Pro
Distanza di messa a fuoco
La pdc è direttamente proporzionale alla distanza di messa a fuoco, cioè se mettiamo a fuoco un punto distante si avrà una pdc maggiore rispetto quella ottenuta mettendo a fuoco un punto vicino della stessa scena (figura 12). Se si considera la macrofotografia, dove si hanno distanze di messa a fuoco molto brevi, si ottengono infatti pdc molto ridotte.
Figura 12 Influenza della distanza di messa a fuoco sulla pdc
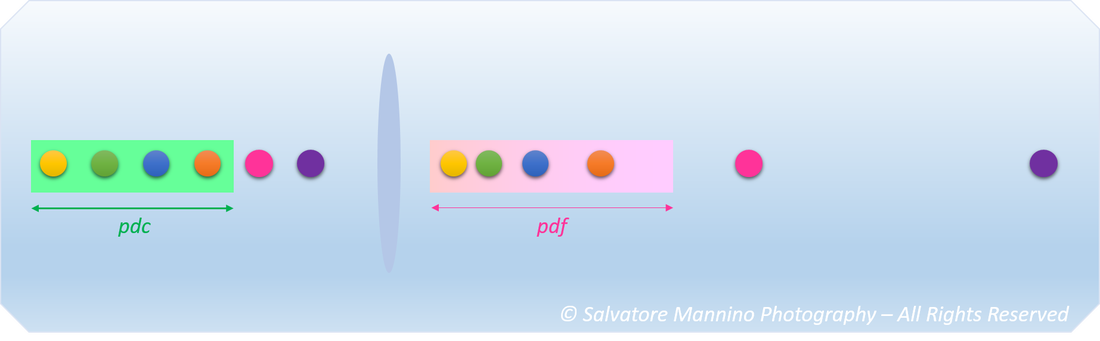
Si presti molta attenzione. Per capirne il motivo, bisogna sapere che oggetti equidistanti, cioè posti ad intervalli regolari, formano le proprie immagini con intervalli irregolari. Come detto in precedenza, oggetti vicini formano le proprie immagini sempre più lontano dalla lente rispetto a oggetti lontani. Si consideri lo schema in figura 13. Si ottiene una compressione degli oggetti più lontani e un distacco sempre maggiore di quelli più vicini.
Figura 13 Rappresentazione schematica della proiezione di punti equidistanti
Definite le condizioni di scatto, se mettiamo a fuoco sul puntino viola, si avrà una profondità di fuoco insufficiente per avere il resto dei puntini nitidi (figura 14).
Figura 14 Rappresentazione schematica dell'influenza di un punto di messa a fuoco prossimo alla lente sulla pdf e sulla pdc
Senza cambiare le condizioni di scatto, se mettessimo a fuoco il puntino più lontano, quello giallo, a parità di pdf si avranno più puntini nitidi (figura 15). In questo modo, la profondità di campo della scena è aumentata.
Figura 15 Rappresentazione schematica dell'influenza di un punto di messa a fuoco lontano dalla lente sulla pdf e sulla pdc
In realtà mettendo a fuoco oggetti più lontani la pdf non rimane inalterata bensì diminuisce, leggermente. Questo effetto ha, comunque, poca influenza sul risultato finale, in quanto risulta essere trascurabile sulla compressione dei piani lontani che, quindi, appaiono a fuoco.
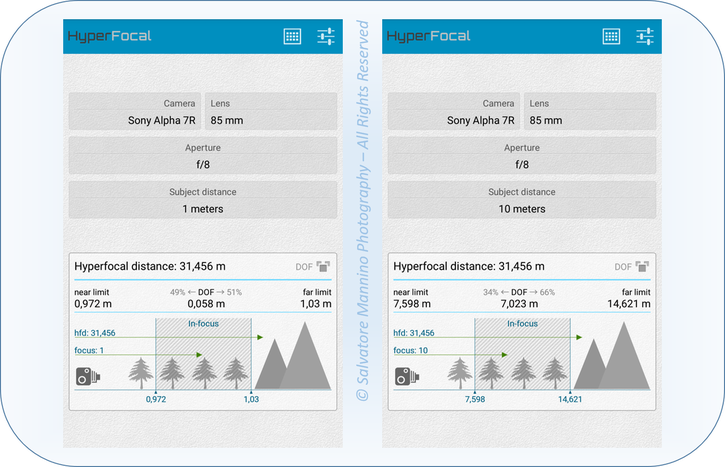
Vediamo un esempio pratico con l’applicazione HyperFocal Pro, come riportato in figura 16. Utilizzando un obbiettivo 85 mm chiuso a f8, si vede come mettendo a fuoco ad 1 metro la pdc ottenuta è molto ridotta, meno di 6 cm (0,058 m). Con le stesse impostazioni, mettendo a fuoco un punto a 10 metri, la pdc aumenta fino a 7,023 metri! Di non minor importanza è da notare anche il cambiamento della distribuzione della pdc attorno il piano di messa fuoco: quando questo si allontana, la pdc di distribuisce sempre più posteriormente (34% anteriore e 66% posteriore) mentre mettendo a fuoco punti vicini, la pdc è sempre più equo-distribuita (49% anteriore e 51% posteriore). PS: Teniamo questi numeri in mente perché il l’argomento sulla pdc vedrà sfatata una famosa legenda metropolitana.
Figura 16 Confronto della scelta della distanza di messa a fuoco tramite HyperFocal Pro
Lunghezza focale
La pdc varia in modo inversamente proporzionale alla lunghezza focale. Questo vuol dire che si avranno pdc maggiori con obbiettivi grandangolari, mentre con i teleobbiettivi è più semplice isolare il soggetto dallo sfondo grazie a pdc ridotte (figura 17).
Figura 17 Influenza della lunghezza focale sulla pdc
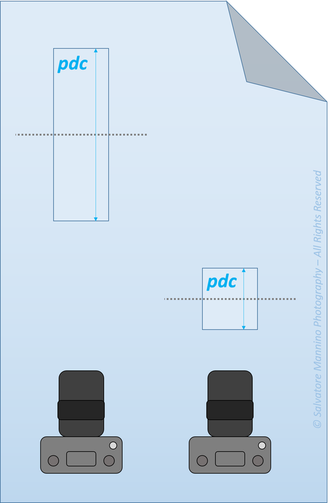
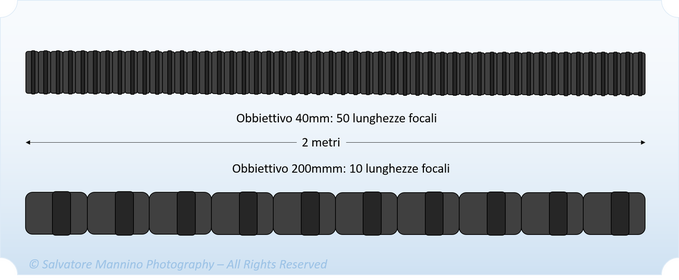
Il motivo di ciò nasce dal fatto che gli obbiettivi misurano lo spazio non in centimetri o metri, come facciamo noi. L’unità di misura è l’obbiettivo stesso. Per una macchina che monta un 50 mm, un oggetto a 10 metri dista l’equivalente di 200 lunghezze focali. Viceversa, lo stesso oggetto posto a 10 metri, per una macchina che monta un 200 mm dista solo 50 lunghezze focali! La figura 18 riporta una schematizzazione di quanto appena detto; per semplicità di disegno sono schematizzati un numero minore di obbiettivi, ma il principio è lo stesso.
Figura 18 Rappresentazione schematica di come un obbiettivo percepisce la realtà in funzione della propria lunghezza focale
La spiegazione è similare a quanto visto precedentemente per la distanza di messa a fuoco. È come se le focali più lunghe vedano il soggetto più vicino rispetto alle focali minori. Bisogna precisare che, in questo caso, non ci si riferisce al concetto teorico di teleobbiettivo e grandangolo. Questo ci spiega perché più è piccolo il sensore, e quindi più è corta la focale dell’obbiettivo maggiore sarà la pdc, cioè sarà più difficile sfuocare lo sfondo. Se si considera una reflex full-frame con una focale di 200 mm, per avere la stessa focale equivalente una fotocamera compatta (con sensore più piccolo) avrà un obbiettivo con una focale minore, ne risulterà una pdc maggiore.
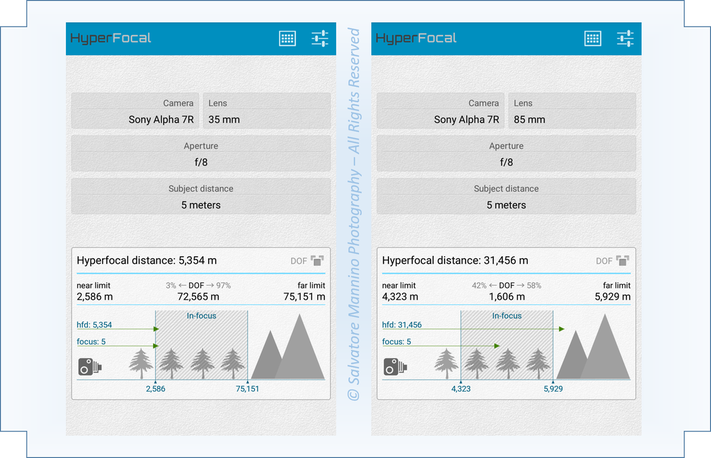
Riporto di seguito le parole del Prof. Enrico Maddalena che, nel 1977, scrisse per un articolo pubblicato sulla rivista “Tutti Fotografi”: “Se misuriamo le distanze prendendo come unità di misura la lunghezza focale, ci rendiamo conto che tutti gli obiettivi si comportano alla stessa maniera. L’obiettivo ancora una volta ci mostra la sua originalità. Lui se ne infischia del nostro sistema metrico decimale: misura il mondo commisurandolo a se stesso ed in questo non si comporta affatto... obiettivamente. È come se per un obiettivo da 100 mm il mondo fosse più piccolo, con dimensioni ridotte della metà rispetto ad un obiettivo da 50 mm, mentre per un grandangolo da 28 mm le cose sono più grandi quasi del doppio. Per un 50 mm, 5 metri sono 100 lunghezze focali, mentre per un 135 mm sono solo 37 e per un 28 mm sono ben 180. Per un tele è come se le cose fossero più vicine a lui e pertanto, per l’identico motivo per cui la profondità di campo varia col variare della distanza di messa a fuoco, varia anche in funzione della lunghezza focale dell’obiettivo usato. Novello Protagora, questo essere meccanico sembra volerci dire, con fotografica filosofia: “L’obiettivo è la misura di tutte le cose...”. Vediamo, adesso, alcuni esempi pratici con l’app HyperFocal Pro. Si consideri il caso di una Sony a7r (full-frame), prima con un obiettivo 35 mm e successivamente con un tele 85 mm (figura 19). A parità di apertura diaframma f8 e distanza di messa a fuoco 5 metri, con un 35 mm si ottiene una pdc di 72,565 metri, mentre con l’85 mm essa si riduce a soli 1,606 metri! Ancora una volta, è evidente come la distribuzione di pdc attorno al piano di messa a fuoco varia drasticamente tra il primo e il secondo caso. Stavolta, in funzione della lunghezza focale si ha una il 3% anteriore e il 97% posteriore per il 35 mm, mentre con l’85 mm si ottiene il 42% anteriore e 58% posteriore.
Figura 19 Confronto della scelta della lunghezza focale tramite HyperFocal Pro
È il momento, quindi, di sfatare una pericolosa leggenda metropolitana. Spesso si legge e si dice, soprattutto per chi si approccia per la prima volta al mondo della fotografia, che “è meglio mettere a fuoco a circa un terzo della scena perché si avrà bene a fuoco un terzo prima e due terzi dopo il piano di messa a fuoco”. Nulla di più sbagliato! Come abbiamo visto per ciascun esempio sopra, questo non è per nulla vero. Le porzioni di spazio nitide attorno al piano di messa a fuoco variano continuamente in funzione dei parametri scelti e dell’attrezzatura in uso. Secondo quanto detto, si può avere una equi-ripartizione delle due porzioni per distanze di messa a fuoco molto vicine, che cambiano secondo tutti i rapporti possibili, con la porzione posteriore che aumenta sempre più rispetto a quella anteriore, con andamento esponenziale, fino ad infinito.
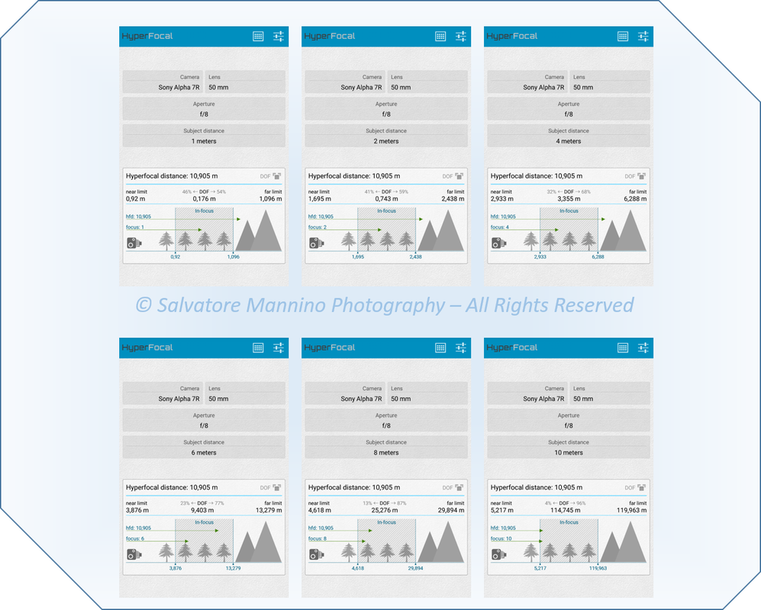
Utilizziamo sempre la stessa Sony a7r con su montato un 50 mm e chiudiamolo a f8. In figura 20 vengono riportati alcuni dati ottenuti tramite HyperFocal Pro per varie distanze di messa a fuoco, ad intervalli regolari di 2 metri fino a 10 (non superiamo la lunghezza iperfocale per cui il piano posteriore si sposta a infinito, come detto tratteremo questo argomento successivamente). Si evince che, per variazioni lineari della distanza di messa a fuoco, la variazione delle proporzioni di fuoco prima e dopo il piano focale non è lineare bensì esponenziale, a vantaggio della porzione posteriore.
Figura 20 Dati delle porzioni anteriori e posteriori della pdc in funzione della distanza di messa a fuoco tramite HyperFocal Pro
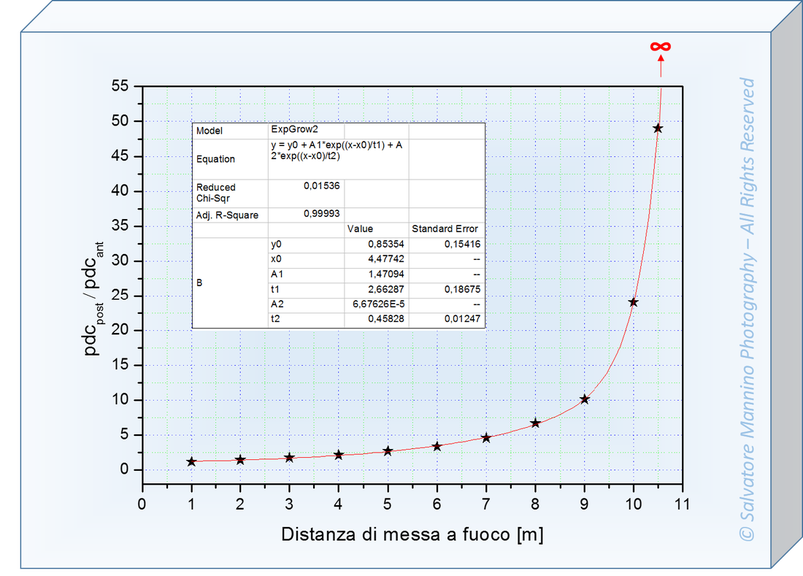
Raccogliendo i dati per ogni metro di messa a fuoco, riportiamo in grafico il rapporto tra la porzione posteriore e quella anteriore della pdc, contro distanza di messa a fuoco. La figura 21 mostra che il fitting che meglio descrive tali punti segue l'equazione di una funzione esponenziale crescente. Da notare che mettendo a fuoco a 10 metri si ha una estensione della pdc per il 96% dopo tale piano cioè un rapporto di 24 (96/4=24), mentre mettendo a fuoco a 10,5 metri (appena 0,5 metri dopo) tale rapporto raddoppia a 49 avendo una percentuale di pdc posteriore del 98% (98/2=49).
Figura 21 Grafico dell'equazione matematica della distribuzione della pdc attorno il piano di fuoco con andamento esponenziale in funzione della distanza di messa a fuoco
Influenza delle dimensioni del sensore o della pellicola sulla pdc
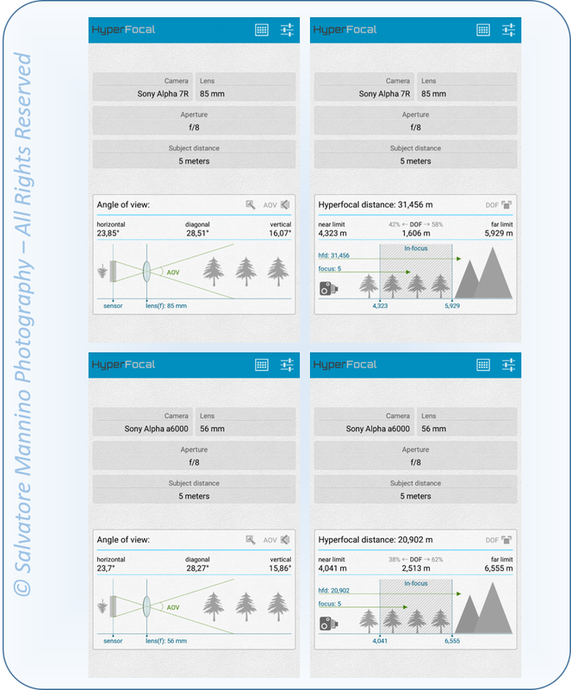
Finora abbiamo visto il significato della profondità di campo e spiegato i fenomeni che determinano il così detto triangolo della pdc. In realtà, esiste ancora una quarta variabile di cui non si è tenuto conto ma che si è solo accennata. Si sta parlando dell’oggetto che registra ciò che attraversa la lente: la pellicola per l’analogico o il sensore per il digitale. In particolare, è la dimensione di questi che ha influenze sulla pdc. Nel mondo delle reflex digitali, i sensori più comuni sono quelli a pieno formato (o full-frame) e quelli a formato ridotto (aps-c) in cui, nella maggior parte dei casi, intercorre un fattore di proporzione pari a 1,5. Oggigiorno c’è molta disinformazione sul web. Spesso, capita di leggere che il formato aps-c dà pdc maggiori rispetto al full-frame, e solo un attimo dopo ci si ritrova in discussioni dove, invece, si sostiene che i due formati diano la stessa pdc in quanto, se si ingrandisse il formato ridotto al pieno formato, si avrebbe un ingrandimento anche dei circoli di confusione e quindi una diminuzione della pdc fino ai valori del full-frame. In realtà, ad essere vera è la prima affermazione: il pieno formato dà pdc minori rispetto al formato ridotto aps-c. Il concetto è espandibile a tutti i formati di sensore ma anche di pellicola. Diapositive più grandi danno pdc minori rispetto a diapositive più piccole. Le diapositive di un banco ottico, quindi, daranno pdc ulteriormente minori rispetto alle pellicole del pieno formato. Quanto appena affermato non deriva da particolari simpatie verso l’una o l’altra teoria. Esistono dimostrazioni matematiche che ne sono alla base. Tali dimostrazioni, tuttavia, saranno qui tralasciate e magari riprese in futuro. Per adesso, è più immediato rifarsi ad esempi pratici per meglio comprendere il concetto. Facciamo subito un confronto tra la Sony a7r (full-frame) e la Sony a6000 (aps-c). Montiamo sulla prima il classico 85 mm da ritratti, visto che, forse, l’argomento può interessare maggiormente i ritrattisti. A questa focale, si ha un angolo diagonale di ripresa di 28,51°. Per avere circa lo stesso angolo di ripresa col sensore aps-c della a6000, bisogna avere una focale di 56 mm (56*1,5≈85). In queste condizioni, come mostrato in figura 22, si noti che col pieno formato si ottiene una pdc di 1,606 m, mentre con il formato ridotto si ottiene una pdc maggiore: 2,513 m ovvero quasi 1 metro in più! Questo deriva sia dal discorso visto in precedenza riguardo la dipendenza della pdc dalla focale, ma soprattutto dalla dimensione del sensore.
Figura 22 Confronto dell'influenza della dimensione sensore sulla pdc tramite HyperFocal Pro
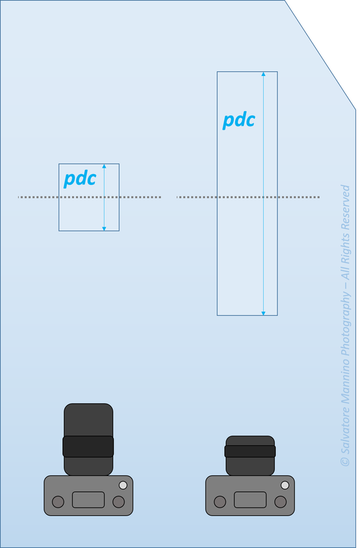
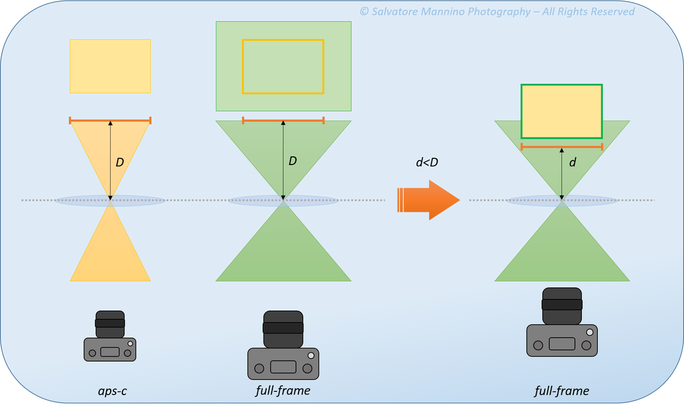
Volendo ancora una volta evitare la dimostrazione matematica, si può sviluppare un ulteriore esempio. Consideriamo il caso in cui sulla Sony a7r e sulla Sony a6000 sia montato lo stesso obiettivo da 85 mm, come mostrato in figura 23. A parità di focale, con il formato aps-c si ha un angolo di ripresa minore, cioè sarà minore la scena inquadrata. Per inquadrare la stessa scena con il pieno formato a parità di focale, bisogna avvicinarsi riducendo la distanza di ripresa a d<D. Sappiamo bene, però, che riducendo la distanza di ripresa si riduce la pdc. Ecco che, a parità di distanza, apertura diaframma e lunghezza focale, la pdc diminuisce con l’aumentare del formato del sensore (o della pellicola).
Figura 23 Rappresentazione schematica dell'influenza della dimensione sensore sulla pdc a parità di lunghezza focale dell'obiettivo
Conclusioni
Quanto visto e discusso in questo articolo vuole servire per comprendere in fondo come le scelte fatte in fase di scatto influenzino il risultato finale. È chiaro che per un fotografo non è indispensabile studiare e conoscere le dimostrazioni matematiche alla base della fisica ottica. Per tale motivo l'argomento è stato affrontato solo con un leggero approccio matematico, al fine di evitare qualsiasi dubbio, e soprattutto con esempi pratici ottenuti con mezzi a portata di tutti come l'app HyperFocal Pro, in modo che chiunque possa sperimentare in prima persona quanto visto ed esaminato. Questo articolo vuole, quindi, essere del materiale d'appoggio valido, non basato sul "sentito dire" bensì nato dallo studio con fondamenta solide, soprattutto per chi si approccia a questo mondo e che può ritrovarsi a commettere degli errori in fase di scatto che poi non saranno rimediabili successivamente in fase di post-produzione. Con la speranza di essere stato il più chiaro possibile, resto a completa disposizione per rispondere alle vostre curiosità.
2 Comments
|
AutoreSalvatore Mannino, fotoamatore dal 2012, dedica molto del suo tempo libero allo studio delle basi e delle tecniche fotografiche. ArchiviCategorie |




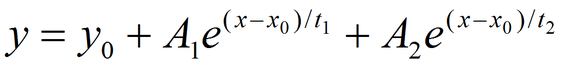
 RSS Feed
RSS Feed
